位置情報を管理し高速に検索する必要がある場合、範囲検索でザックリと絞りこみ、その後にオンメモリで処理する方法が考えられます。 範囲検索でザックリと絞りこむためには、事前に位置情報を一定の範囲で同一となるハッシュ値に変換しておく事で、高速に比較ができるようになります。
位置情報のハッシュ値計算にはGeo Hex, S2等のいくつかの手法が存在しますが、 その中でもPokemon Go等の検索の速度性が求められているサービスでも採用事例が多いにもかかわらず、 ドキュメントの少ないS2ライブラリについてGoに移植されているライブラリを「渋谷駅を中心に半径4kmの円」に含まれるデータを範囲検索するというユースケースを想定して利用してみました。
S2ライブラリとは
S2のライブラリは球面上をレベルと呼ばれる解像度で段階的に細分化していきながら複数の領域(Cellと呼ばれます)に分割していき、 各CellにIDをわりあてるライブラリで、C++でGoogleで最初に開発されたものです。
Google公式の情報としては解説のプレゼンがアップロードされている以外は、 更新がほぼされていないソースコードがGoogle Codeに上がっているのが分かる程度で、ドキュメントはほとんど存在しません。
S2の領域分割やIDのわりあてアルゴリズム解説は
http://blog.christianperone.com/2015/08/googles-s2-geometry-on-the-sphere-cells-and-hilbert-curve/
こちらの記事がわかりやすく、平面ををヒルベルト曲線で埋めていくことや、レベルを跨いだCell間の包含判定が IDの前方一致(厳密には末尾1ビットを削る等の処理は必要だが)で実現できる等の特徴などがわかりやすく解説されています。
S2の機能を提供するGoライブラリ
S2のライブラリはGoにも移植されています
Geoライブラリは:
- 一次元空間をあつかうR1
- 二次元空間をあつかうR2
- 三次元空間をあつかうR3
- 円をあつかうS1
- 球面をあつかうS2
と段階的に複雑な空間を扱うように開発されており、 S2まで段階については移植完了しており、S2は半分ほど移植が完了している段階なようです。
S2で「渋谷駅を中心に半径4kmの円」に含まれるデータを範囲検索する
ここでは、位置情報の検索のユースケースとして「渋谷駅を中心に半径4kmの円」に含まれるデータを検索したいというケースを想定しています。 S2では、球の表面を細かなエリアに分割し、それぞれのエリアにハッシュ値がわりあてられます。
そのため、円にデータが含まれるかどうかを範囲検索するためには:
- S2で「渋谷駅を中心に半径4kmの円」を表現する
- その円と重なっているエリアのハッシュ値を取得する
- 最後にそのハッシュ値を持つデータを絞りこむ
という3つのステップが必要になります。
では、まずS2上で「渋谷駅を中心に半径4kmの円」を表現してみましょう
S2上の「渋谷駅を中心に半径4kmの円」
球面上の円
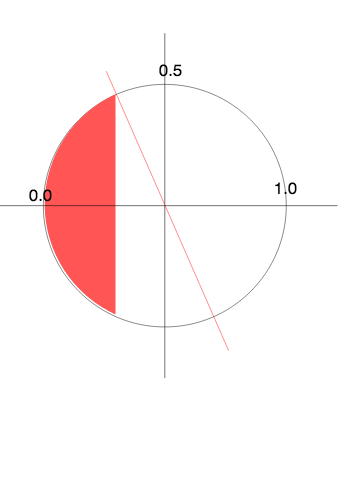
S2で扱う球面上での円は、平面上の円とは違い、球の表面に沿って曲ったキャップのような形状になっています。
そのため、S2では球面上の円はCapという型名とされています。
図ですと、赤い部分が球を大円で切ったときのCapです。
また、S2自体は地球表面のみならず、一般の真球の球面をあつかうライブラリであるため、 球の半径には依存しない、点と点の角度や球の大円に対する比率で相対的にCapを扱っており、球の表面を完全に覆っているときに比率が1となります。
地球上での円をS2で扱う
s2.CapFromCenterAngleという関数でs2.Capを作ることができるのですが、
引数として、キャップの頂点となる球面上の点と、キャップの縁の大円に対する比率を与える必要があります。
S2が球の半径には依存しないため、たとえば実際にユースケースとして「渋谷駅を中心に半径4kmの円」を想定した場合には、
地球のサイズの球からの相対的な比率計算をする必要があります。
ここで、仮に地球の半径を6371.01kmと置くと、半径4kmの円の比率は4 / 6371.01になります。
そのためキロメートルを指定して地球上の円を作成するためには以下のような関数を定義する必要があります:
func capOnEarth(center s2.Point, radiusKm float64) s2.Cap { const earthRadiusKm = 6371.01 ratio := (radiusKm / earthRadiusKm) return s2.CapFromCenterAngle(center, s1.Angle(ratio)) }
すると、「渋谷駅を中心に半径4kmの円」は以下のように生成する事ができるようになりました:
shibuya := s2.LatLngFromDegrees(35.658034, 139.701636) shibuyaCircle := capOnEarth(s2.PointFromLatLng(shibuya), 4)
円と重なっているエリアのハッシュ値を取得する
次は、生成した「渋谷駅を中心に半径4kmの円」と重なっているエリアのハッシュ値を取得してみましょう。 そのような目的のためにRegionCovererという構造体が提供されており、指定された図形をで埋めるハッシュ値のリストを計算できます。
S2では、球面をどのようなサイズのエリアに分割するのかの解像度をLevelとして扱っています。 詳しい各レベルでのエリアサイズは冒頭の公式のプレゼンを見ていただければ幸いですが、
RegionCovererの生成時に
MaxLevel: 30と指定する事で、S2が扱う事ができる最大の解像度を利用するように指定MaxCells: 50と指定する事で、被覆するにの利用してよいCellの最大数
を指定しています。
rc := &s2.RegionCoverer{MaxLevel: 30, MaxCells: 50}
for idx, c := range rc.Covering(shibuyaCircle) {
cell := s2.CellFromCellID(c)
fmt.Printf("Cell [%d] vertex:\n", idx)
for i := 0; i < 4; i++ {
v := cell.Vertex(i)
latLng := s2.LatLngFromPoint(v)
fmt.Printf("{lat: %v, lng: %v}\n", latLng.Lat, latLng.Lng)
}
}
このようにする事で、円を覆うのに利用されたCellのIDと、そのCellの4つの頂点の座標のリストを手にいれる事ができます。
円の被覆の精度とのトレードオフ
もちろんレベルを最大まで利用できるとし、仕様可能なセル数も増やすとより厳密に円を被覆できるようになりますが、 その分データを検索する対象となるセルIDの個数が増える事になるため、トレードオフとなります。 そこで、最小のレベルまで利用できるという設定は変えずに、仕様可能なセルの個数を段階的に50 -> 100 -> 200と増やしながら Google Map上に表示してみて、実際の円との一致度合いと利用されるセルの個数を確認してみましょう。
Google Map上でCellを表示し、被覆の度合いを可視化
青色の円(重なっているので紫ですが)は GoogleMapの機能で渋谷駅から半径4kmを描いてみたものです。
セル上限50の場合
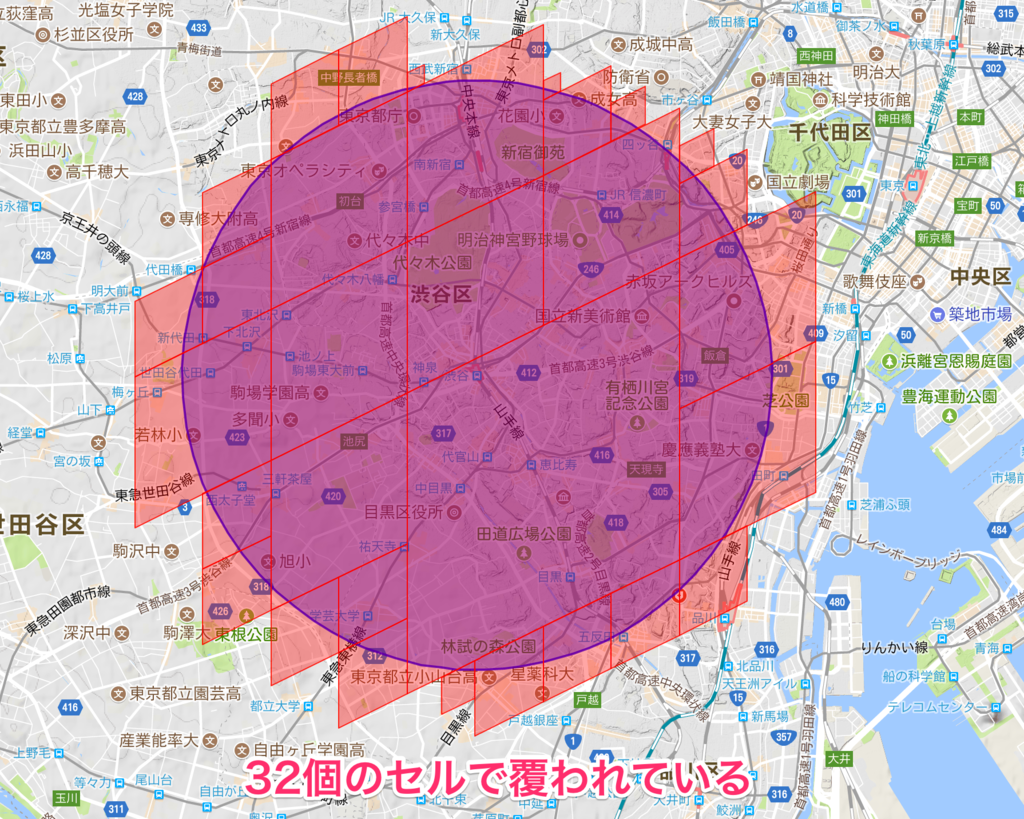
結構はみ出しているところが目立ちますね 利用されているセルは32個となりました
セル上限100の場合
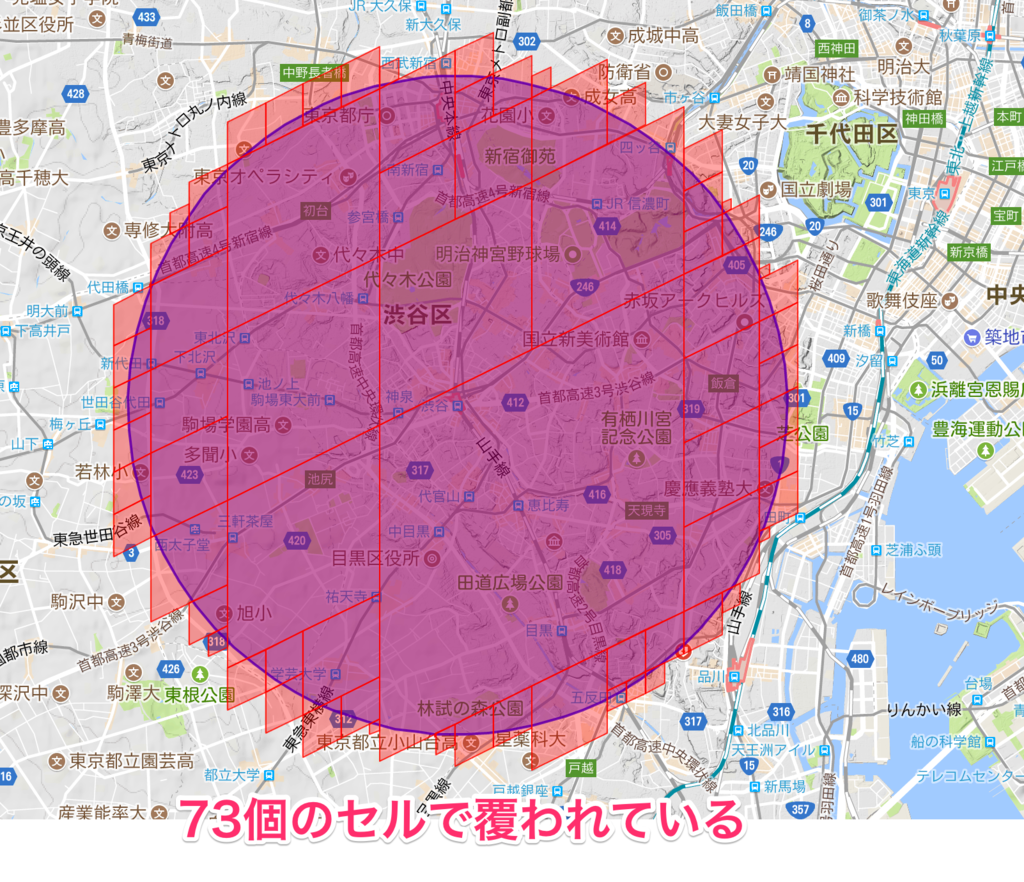
すこしはみ出しが減りました。 利用されているセルは73個となりました
セル上限200の場合
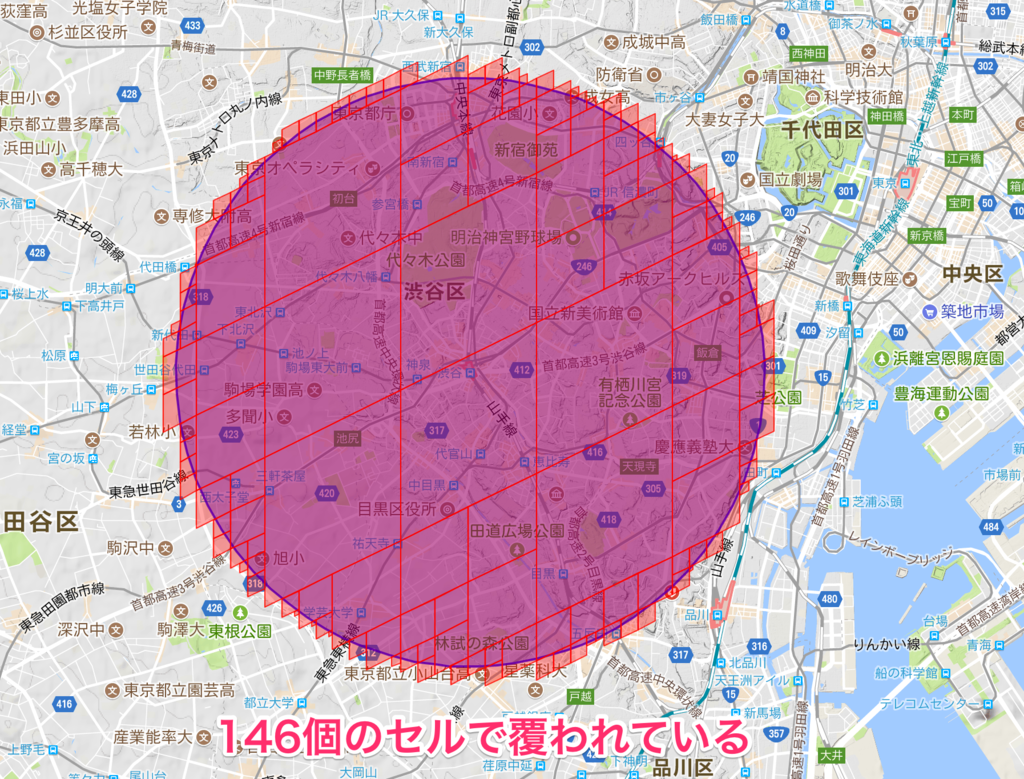
かなりはみ出しが改善しました。 利用されているセルは倍以上の146個となりました